Learning Checklist
Understanding Simultaneous Equations
Examples
Linear Simultaneous Equations
What are linear simultaneous equations?
- When there are two unknowns (say x and y) in a problem, we need two equations to be able to find them both: these are called simultaneous equations
- you solve two equations to find two unknowns, x and y
- for example, 3x + 2y = 11 and 2x – y = 5
- the solutions are x = 3 and y = 1
- you solve two equations to find two unknowns, x and y
- If they just have x and y in them (no x2 or y2 or xy etc) then they are linear simultaneous equations
How do we solve linear simultaneous equations by elimination method?
- “Elimination” completely removes one of the variables, x or y
- To eliminate the x‘s from 3x + 2y = 11 and 2x – y = 5
- Multiply every term in the first equation by 2
- 6x + 4y = 22
- Multiply every term in the second equation by 3
- 6x – 3y = 15
- Subtract the second result from the first to eliminate the 6x’s, leaving 4y – (-3y) = 22 – 15, i.e. 7y = 7
- Solve to find y (y = 1) then substitute y = 1 back into either original equation to find x (x = 3)
- Multiply every term in the first equation by 2
- Alternatively, to eliminate the y‘s from 3x + 2y = 11 and 2x – y = 5
- Multiply every term in the second equation by 2
- 4x – 2y = 10
- Add this result to the first equation to eliminate the 2y‘s (as 2y + (-2y) = 0)
- The process then continues as above
- Multiply every term in the second equation by 2
- Check your final solutions satisfy both equations
How do we solve linear simultaneous equations by the substitution method?
- “Substitution” means substituting one equation into the other
- Solve 3x + 2y = 11 and 2x – y = 5 by substitution
- Rearrange one of the equation into y = … (or x = …)
- For example, the second equation becomes y = 2x – 5
- Substitute this into the first equation (replace all y‘s with 2x – 5 in brackets)
- 3x + 2(2x – 5) = 11
- Solve this equation to find x (x = 3), then substitute x = 3 into y = 2x – 5 to find y (y = 1)
- Rearrange one of the equation into y = … (or x = …)
- Check your final solutions satisfy both equations
How do we solve linear simultaneous equations by graphical method?
- Plot both equations on the same set of axes
- to do this, you can use a table of values or rearrange it into y = mx + c if that helps.
- Find where the lines intersect (cross over)
- The x and y solutions to the simultaneous equations are the x and y coordinates of the point of intersection
- e.g. to solve 2x – y = 3 and 3x + y = 4 simultaneously, first plot them both (see graph)
- find the point of intersection, (2, 1)
- the solution is x = 2 and y =
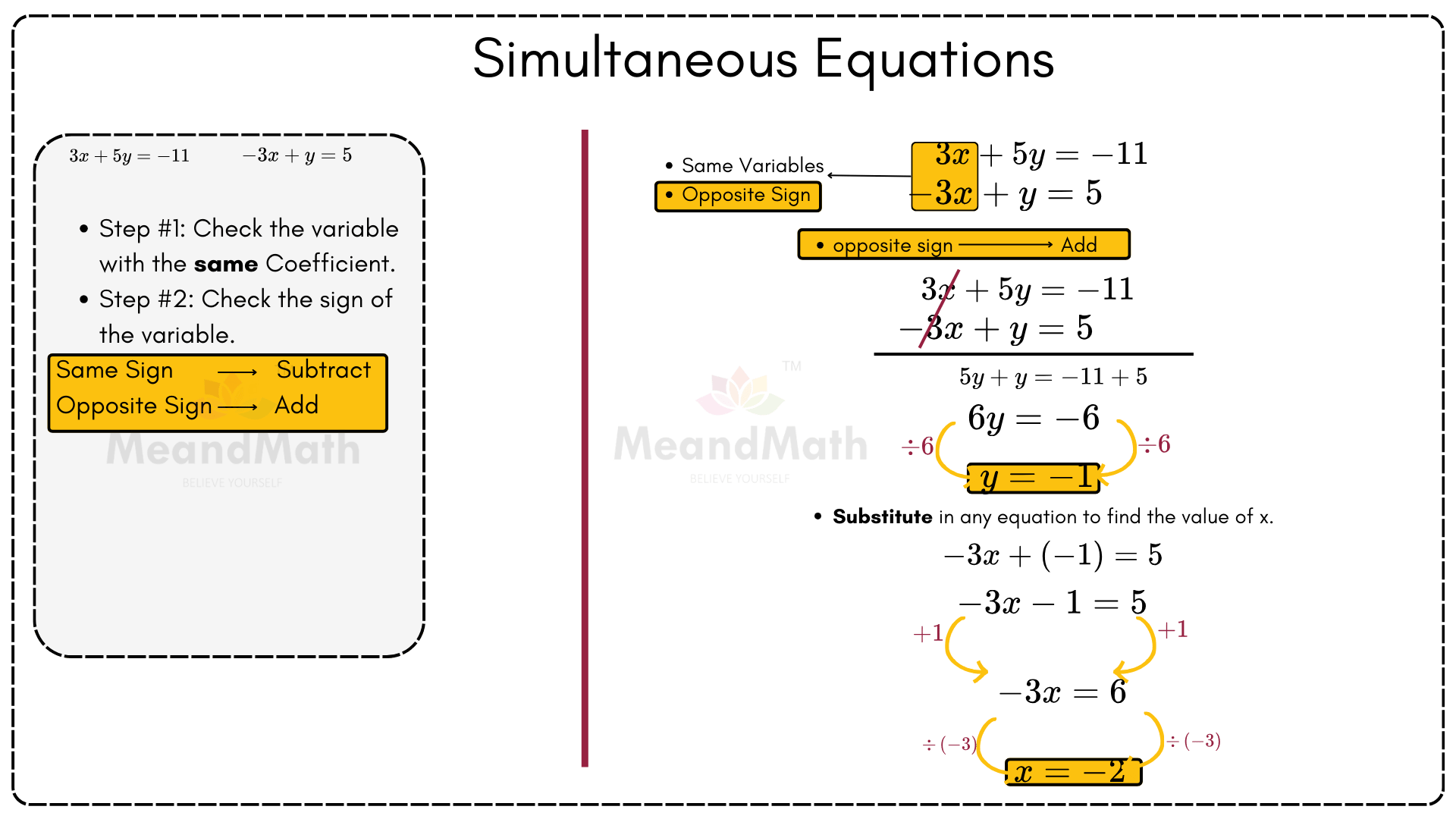
Examples
Solve the simultaneous equations
5x + 2y = 11
4x – 3y = 18
Number the equations.
5x + 2y = 11 ——->1
4x – 3y = 18 ——->2
Make the y terms equal by multiplying all parts of equation (1) by 3 and all parts of equation (2) by 2.
This will give two 6y terms with different signs. The question could also be done by making the x terms equal by multiplying all parts of equation (1) by 4 and all parts of equation (2) by 5, and subtracting the equations.
15x + 6y = 33 ——->3
4x – 3y = 18 ——->4
The 6y terms have different signs, so they can be eliminated by adding equation (4) to equation (3).
15x + 6y = 33
+(4x – 3y = 18)
_______________
19x=
Examples:











Test Your Understanding
Olympiad Level Questions
Practice Quiz(download meandmath practice app)
Still Stuck!
Book a free demo class & clear your doubts!
Related Topics
- Understanding Whole as a Percentage
- Simplifying Percentages
- FDP
- Finding 10%
- Finding 5%
- Finding % of an amount
- Percentage Increase & Decrease
Learning Checklist
- Understanding Percentages
- Percentage symbol
- Understanding percentages visually
Understanding Percentage
A percentage is a number that is expressed as a part of 100.
Per means Out Of, & cent means 100.

Let’s discuss more.
5% means 5 out of 100.
12% means 12 out of 100.
Let's learn through visuals.

Examples
A percentage can be represented by shading in a 100 square grid.





Test Your Understanding
Olympiad Level Questions
Practice Quiz(download meandmath practice app)
Still Stuck!
Book a free demo class & clear your doubts!
Related Topics
- Understanding Whole as a Percentage
- Simplifying Percentages
- FDP
- Finding 10%
- Finding 5%
- Finding % of an amount
- Percentage Increase & Decrease

